Zenon kaže (1.) da je Ahilu potrebno beskonačno mnogo ”koraka”, što podrazumijeva (2.) da mu za njih treba beskonačno mnogo vremena. Slijedi li nužno (2.) iz (1.)? Je li moguće da mu je za beskonačno mnogo ”koraka” dovoljno konačno mnogo vremena?
Komentator na Ahilu i kornjači, pod nadimkom Kairos, kaže:
Ovo je problem zbrajanja beskonačne serije … Ovo je matematički način rješavanja ovakvih paradoksa gdje se zbrajaju sve manji dijelovi beskonačno mnogo puta.
Dakle, izgleda da nam treba neko znanje iz matematike. U hrvatskom je u ovome matematičkom značenju za englesko series uobičajena riječ ”red”. Zbroj beskonačnog reda se uči iz matematike u 4. razredu, pa ga velika većina čitatelja još nije učila. Ovdje ću pojednostavljeno objasniti one zamisli koje su nam (možda?) potrebne za pitanje o Ahilu i kornjači. Naravno, iz matematike ćete redove učiti na pravi, strogi način.
Mora li zbroj beskonačno mnogo članova biti beskonačan?
Recimo zbroj 1 + 1 + 1 + … očito ide u beskonačno. Isto tako i zbroj 1 + 2 + 4 + 8 +… Vrijedi li to za svaki zbroj beskonačno mnogo članova? Znalaoc kaže:
… ako počnemo dijeliti tu duljinu na sve manje dijelove dođemo do zaključka da je taj prostor beskonačno djeljiv, znači beskonačan je…
Dakle, ako neka duljina ima beskonačno mnogo dijelova, onda je beskonačna? Ili nije? Kairos naglašava da ”se zbrajaju sve manji dijelovi”. Na primjer, je li ovaj zbroj beskonačan?
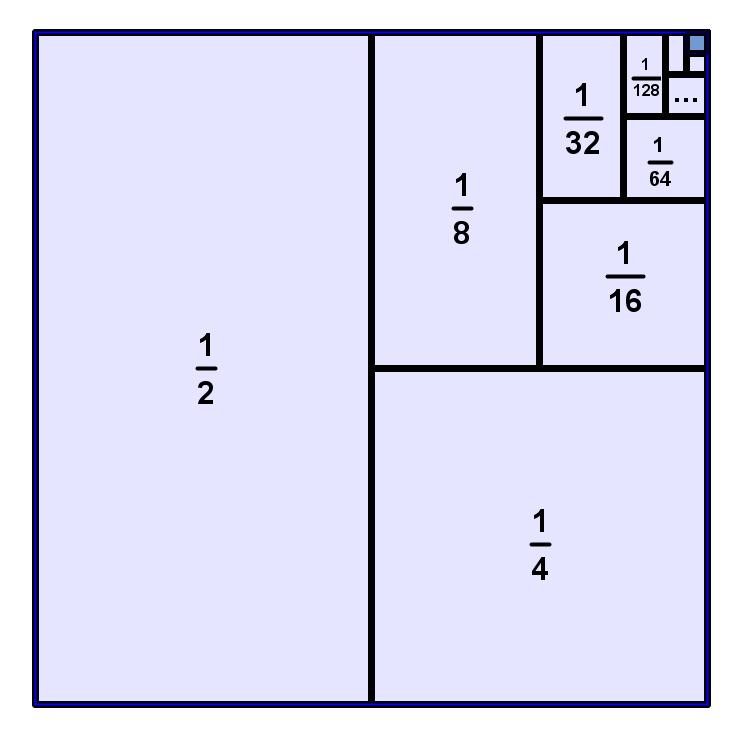
Ne! Slika dovoljno govori:
Površina gornjeg lika očito nije beskonačna, mada ima beskonačno mnogo dijelova.  ima beskonačno mnogo članova, ali, budući da su ti članovi sve manji i manji, suma je konačna. U ovom slučaju, kao što se vidi iz slike, iznos sume je 1.
ima beskonačno mnogo članova, ali, budući da su ti članovi sve manji i manji, suma je konačna. U ovom slučaju, kao što se vidi iz slike, iznos sume je 1.
(Ili je ipak malo manji od 1? 😉 )
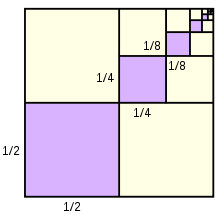
Evo još jednog primjera:
Dokaz:
Budući da površina gornjeg kvadrata očito nije beskonačna, jasno je da je suma konačan broj, bez obzira što je članova beskonačno mnogo. Vidite li iz slike da je ta suma 1/3? (Ili je stalno sve manje, ali uvijek još malo, malo, malo,… manja od 1/3? ;))
Dakle, moguće je zbrojiti beskonačno mnogo (sve manjih!) dijelova i dobiti konačan broj.
Sad, neki kažu da je se zbroj  uvijek sve više približava iznosu 1, ali da nikad nije 1! Sigurno je da taj zbroj nije veći od 1 (svakako nije beskonačan). Ali je li 1 ili je malo manji od 1? Svaki novi pravokutnikić na ovoj slici približava površinu iznosu 1, ali nakon koliko pravokutnika će ona zapravo biti 1?
uvijek sve više približava iznosu 1, ali da nikad nije 1! Sigurno je da taj zbroj nije veći od 1 (svakako nije beskonačan). Ali je li 1 ili je malo manji od 1? Svaki novi pravokutnikić na ovoj slici približava površinu iznosu 1, ali nakon koliko pravokutnika će ona zapravo biti 1?
Da bi površina bila upravo 1, a ne skoro 1, potrebno je dodati beskonačno mnogo pravokutnikića. Što vi mislite, je li OK reći: jasno se vidi da na kraju suma mora biti 1, ili ipak treba cjepidlačiti s time da nema kraja nego se površina uvijek samo približava 1?
I, glavno pitanje: rješava li ovo Ahila i kornjaču?
Ako zbrojimo sve manja vremena t1 + t2 + t3 +… dobijemo li konačan ili beskonačan rezultat? Ako je konačan, što mislite je li taj rezultat jednak rezultatu kojega dobijemo ispravnim fizikalnim računom? Ako nije jednak, je li puno veći ili malo manji od fizikalno ispravnoga?
hnjo kaže:
mislim da je problem u tome što ovim načinom se vrijeme sve više smanjuje, i kad zbrojimo sve t-ove (beskonačno ih je) nikad nećemo dobiti ono vrijeme u kojemu će se oni susresti, a to je 10 sekundi
Što vi kažete? 🙂
Dodatak: Možemo izvesti formulu za računanje sume beskonačnog reda, kad su članovi po iznosu manji od 1. Općenito, suma 1 + x + x2 + x3 + … ima konačan rezultat ako je iznos x manji od 1. (Vidjeli smo da je npr. za vrijednosti x =1 ili x =2 ta suma beskonačna.) Kolika je ta suma? Recimo da je S. Dakle,
S = 1 + x + x2 + x3 + …
Sad pomnožimo obje strane jednakosti sa x.
S∙x = x + x2 + x3 + x4 + …
S desne strane to je isti izraz kao i ranije, samo bez 1! (Je li? 😉 ) Dakle
S = S∙x + 1
S – S∙x = 1
S∙(1-x) = 1
i na kraju
(Dobijemo li za vrijednosti x = 1/2 i za x = 1/4 pomoću gornje formule iste rezultate kao što smo ranije dobili pomoću slika? Možemo li ovu formulu primijeniti na problem Ahila i kornjače?)
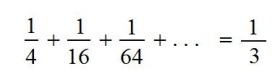


Odgovori na Luka M Otkaži odgovor